The Warwick-Imperial Mathematics Conference (WIMP) will take place on Saturday 1 March. The itinerary is as follows:
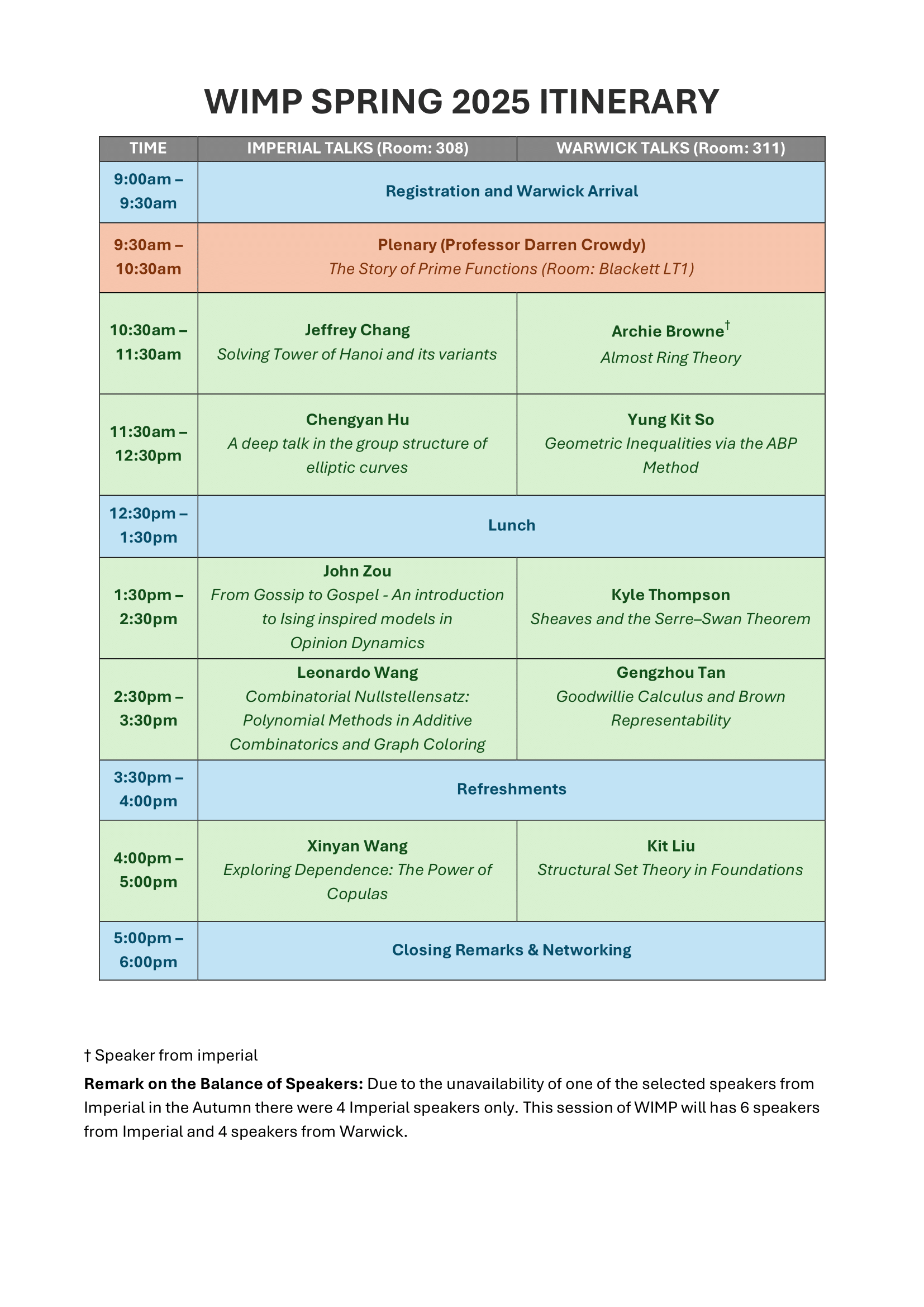
Abstracts for the student talks can be found below.
The plenary talk will be given by Professor Darren Crowdy, from 0930 to 1030 in Blackett LT1.
Title: The Story of Prime Functions
Abstract:
Every undergraduate mathematician has used so-called “prime functions” many times, usually without knowing it. This talk aims to show that this class of functions are ubiquitous in mathematics, are especially useful in applications, and that their significance has historically been overlooked. The presentation should be accessible to most undergraduate and graduate students in mathematics.
Student talk abstracts
Warwick talks
Yung Kit So (Geometric Inequalities via the ABP Method):
In this talk, I will discuss how the Alexandrov-Bakelman-Pucci (ABP) method, which recently became a popular tool for proving geometric inequalities, can be used to prove the isoperimetric inequality and the Sobolev inequality on manifolds with nonnegative Ricci curvature. I will explain the key steps of the ABP method, including the construction of the lower contact set, the use of normal mapping, and the role of convexity. I will also highlight why the ABP method is naturally suited for such proofs, as it connects to the ABP maximum principle and has natural geometric visualisation. To illustrate, I will first present a simple example: proving the isoperimetric inequality in R^n following Cabré’s proof. Then, I will explain how Brendle’s proof of the Sobolev inequality extends the ABP method to curved spaces (manifolds) by modifying the convexity condition to account for curvature. This talk will show how the ABP method links local function properties to global geometric and analytic results, demonstrating the power of intuitive geometric reasoning.
Kyle Thompson (Sheaves and the Serre-Swan Theorem):
What is geometry? The study of shapes. What’s a shape? A space with some structure. What structure? A sheaf. Sheaves arise in mathematics all over the place, from geometry to logic, and – while complicated – they arise from the simple goal of studying the functions on a space. This talk focusses on studying the most basic applications of sheaves to construct the natural category in which to do geometry: the category of locally ringed spaces. Additionally, once we have a space, we care about what are called “vector bundles” over this space – objects constructed by taking a space and attaching a vector space to each point. By viewing these objects in terms of sheaves we can gain insight into their algebraic structure by introducing the powerful so-called Serre–Swan theorem. A theorem that has applications to topology, differential geometry, and algebraic geometry, giving us a comprehensive characterisation of the possible vector bundles we can define over any (reasonably nice) space.
Gengzhou Tan (Goodwillie Calculus and Brown Representability):
We know from Brown Representability (Brown \(1962\)) that every generalized cohomology functor is representable from homotopy category to category of abelian group. Moreover, this sequence of spaces that represents a particular cohomology theory can be connected through a structure map and form a new topological object called spectrum. However, spectra contain generally more information than cohomology theories. More precisely, there might be more than one spectrum which represents a single cohomology theory (namely the phantom map). In this talk, we present a new way to correspond category of spectra with a special kind of functor, linear functor. This correspondence is finer than generalized cohomology theory in the way that the category of linear functor classifies spectra completely in a bijective correspondence. The way to define this functor relies on the theory of functor calculus which was first introduced by Goodwillie in a series of paper around \(2000\). Ideally, I will first introduce basic notions in Goodwillie Calculus and its analogy to ordinary calculus. Later, I will use notions we have developed to prove the correspondence between linear functor and spectra.
Kit Liu (Structural Set Theory in Foundations):
Suppose you were asked, “is \(3 \in \mathbb{N}\)?” Being a natural number, \(3\) is indeed a member of \(\mathbb{N}\), so the answer is “yes”. On the other hand, the question, “is \(\pi \in \mathbb{Q}\)?”, would quickly receive an answer of “no”. Now, suppose you were then asked, “is \(\pi \in \log\)?”
You’d might pause for a moment, before again answering in the negative, but for a different reason than before. After all, \(\pi\) is a number, and \(\log\) is a function, so \(\\pi\) being a member of \(\log\) – whatever that means – would be ridiculous! A better answer might be to declare the question as meaningless.
However, in the standard foundational framework of ZFC – Zermelo–Fraenkel set theory with Choice – everything is a set, so the question “is \(\pi \in \log\)?” should have a yes-or-no answer. This viewpoint is at odds with how most mathematicians use sets in practice: we don’t usually think of functions (or many other objects) as sets, because they’re not meaningfully compatible with set operations nor relations, and the truth value of propositions involving these operations or relations applied to objects typically not considered to be sets depend purely on (arbitrary choices of) implementation details and will generally fail to be isomorphism invariant.
Many of these quirks arise from the “global” nature of the set membership relation: it is always valid to compare any two arbitrary sets for membership and equality. However, in most practical contexts, sets are often stratified, in the sense that we usually don’t have very long chains of membership containment, and sets from different strata are very rarely compared or combined.
In this talk, we present the structuralist’s solution to this problem: a way of formulating the foundations of mathematics that more closely resembles how mathematicians actually manipulate sets in practice, by constructing “structural” sets connected together via local set membership relations between them.
Imperial talks (Room 308)
Archie Brown (Almost Ring Theory):
Originally introduced by Faltings, almost Ring Theory is a formal relaxation of the axioms of standard comutative algebra. It has since been developed mainly by Gaber and Ramero in their comprehensive textbook and famously utilised to great extend by Scholze in his Fields medal winning work on Perfectoid spaces. Somewhere between commutative algebra and category theory, Almost Mathematics is a major generalisation of much of the algebra which we learn. As such, it provides insights and novel techniques for proving a lot of classical results. Practically every object or theorem you know in commutative algebra has an almost counterpart. This talk will bring you up to speed on the basic definitions and ideas of the field before taking a glance at some of the new results I am attempting to work on. This mainly includes calculations of the Grothendieck group for certain classes of “almost” modules.
Jeffrey Chang (Solving Tower of Hanoi and it’s variants):
This talk will explore the Tower of Hanoi and its two variants—the Cyclic and Linear Hanoi—focusing on the minimum moves required for each. We will discuss the recursive strategies behind solving these puzzles and how additional constraints affect complexity. The aim is to provide a clear mathematical framework for understanding these problems while making the content accessible to a broad audience, including those with minimal mathematical background. Visual demonstrations and step-by-step breakdowns will ensure clarity. By the end, attendees will grasp both the theoretical and practical aspects of these puzzles, appreciating their algorithmic and problem-solving significance.
Chengyan Hu (A deep talk in the group structure of elliptic curves):
I treat this talk as an introduction to the area of elliptic curves, aiming to prove the group of rational points on an elliptic curve is finitely generated (Mordell-Weils Theorem), with as few pre-requirement (essentially only basic group theory) as possible. We will take a more algebraic approach to the group structure, using the Cayley-Bacharach Theorem to establish associativity and avoid cumbersome computations. Next, we will discuss the criteria for an abelian group to be finitely generated, which is purely a group theoretic result, laying the groundwork for the Weak Mordell-Weil Theorem. Using a specific elliptic curve \(y^2=x(x-1)(x+1)\) as example, the idea of proof will be clear, so the formal proof can be left as an easy exercise. With the help of a height function (which will be discussed), Mordell-weils will be done. Finally, we will briefly introduce abelian varieties as a natural generalization of elliptic curves.
John Zou (From Gossip to Gospel: An Introduction to Ising inspired models in Opinion Dynamics):
Understanding how opinions evolve in a society is a central challenge in social science, with applications ranging from political polarization to the spread of misinformation. Predicting individual opinions is challenging, however, techniques from statistical mechanics allow predictions of collective behaviour despite individual unpredictability. In this talk we will explore opinion dynamics using Ising-like models, introducing some well-known models including the voter model and the majority rule model. We will use the context of rumour spreading on a random graph and present findings using numerical methods such as Monte-Carlo simulations to analyse the emergence of consensus. Through this interdisciplinary lens, we aim to highlight how mathematical physics can provide insights into real-world social dynamics.
Leonardo Wang (Combinatorial Nullstellensatz: Polynomial Methods in Additive Combinatorics and Graph Coloring):
A spin-off, and in some ways a stronger version of Hilbert’s Nullstellensatz in Algebraic Geometry, the methodology of Combinatorial Nullstellensatz relies on the ingenious idea of embedding information - often about sets or graphs - in a polynomial. Often, through exploiting the finiteness of its zero set and by maneuvering its degree, one can prove existence magically - even though such an existence is non-constructive, one can still extract an immense amount of information through this algebraic technique. In this talk, I will introduce the theorem and explore its applications in two areas: graph coloring and additive combinatorics. I’ll first demonstrate its prominent role in additive combinatorics, including zero-sum problems and sum-set inequalities. Then I will showcase its use in proving the existence of proper graph colorings, with applications in identifying degree of choosability of graphs as well as hypergraph coloring and more. Overall, this talk will highlight how polynomial methods provide a unifying framework for diverse combinatorial problems.
Xinyan Wang (Exploring Dependence: The Power of Copulas):
Traditional methods like linear regression and multivariate distributions often struggle to find non-linear dependencies and tail risks. This talk will introduce copulas as a powerful alternative for modeling complex dependency between datasets. We’ll start by introducing different correlation coefficients, including Pearson’s rho and Kendall’s tau. Then explore Sklar’s theorem and the role of copulas in multivariate analysis. In a discussion of a bivariate Gaussian copula, its mathematical basis, estimation of its parameters, and fitting in practice will then be discussed. Other copula types, such as Archimedean and \(t\)-Copula, and use with continuous and discrete data will then follow.